AI Safety Fundamentals - Polysemanticity vs Superposition

Reconciling two different definitions of "superposition" in mechanistic interpretability

Introduction

I recently finished taking part in the AI Safety Fundamentals course. This course gives a broad overview of many of the different areas of AI safety. Each week, you dive into some readings on a particular topic—like RLHF, scalable oversight, or AI governance—do some simple writing exercises, and then meet with your weekly group to discuss and debate everything you learned.

Mechanistic Interpretability

One week, our topic was mechanistic interpretability. Among other things, we read the Zoom In: An Introduction to Circuits paper from OpenAI and bits of Anthropic’s Toy Models of Superposition. In my discussion group, we ended up having some confusion and disagreement about what exactly the difference is between “polysemanticity” and “superposition”. I’ve since done a bit of digging to sort this out.

Okay, I should back up a bit. If you don’t know, mechanistic interpretability is all about trying to decode and understand neural networks. In a very significant sense, you can think of modern AI systems as “grown”, rather than engineered. We typically imagine that engineers deeply understand the systems they build, which is how they manage to build them in the first place. But we have no illusions that a gardener understands all the biological mechanisms underlying the plants they grow. (At least, not well enough to bioengineer plants that do what they want.)

The latter is much closer to our position with respect to understanding current AI systems. We train elaborate networks which can do amazing things, but we have very little idea of how or why they do what they do. This seems bad if you want to have precise control over them.

Mechanistic interpretability aims to truly understand neural networks, to figure out the precise algorithms they are running and fully reverse-engineer their operation in a way that makes sense to us. This is an ambitious goal, and the field is still quite young, so for the most part they’re starting with smaller goals. The Zoom In paper is probably the most foundational piece of research in this area.

It’s part of a larger thread of papers which aim to reverse-engineer convolutional neural networks for vision. The paper introduces many of the core concepts in mechanistic interpretability, like features and circuits.

At a high level, features are coherent concepts found in the neural network’s inputs which the model is able to internally represent and use. Features vary from low-level ones such as curves, to high-level ones like dogs. A circuit is a set of interconnected neurons which combine features in some way to form new features.

Polysemanticity and Superposition

Zoom In discusses another two important concepts: polysemanticity and superposition. Polysemanticity is pretty easy to understand, although the phenomenon itself may seem strange at first. It’s when a neuron activates in response to multiple distinct features. The paper gives an example of a neuron which responds to images of both cars and cats. See below for the features which maximally stimulate the neuron:

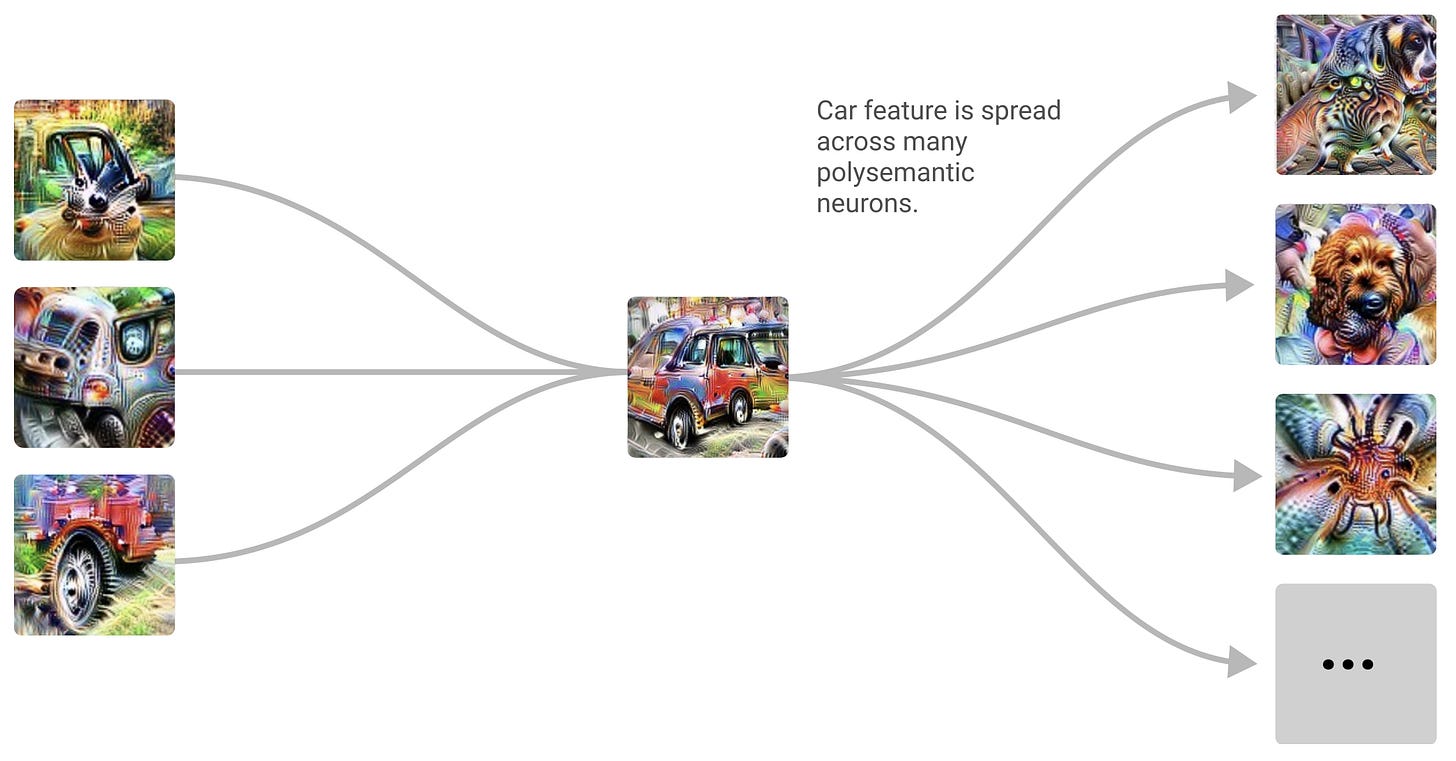
Superposition is also seemingly not too hard to get. The paper says superposition is “where a circuit spreads a feature across many neurons, presumably to pack more features into the limited number of neurons it has available”. They provide the following visualization:

Along the left, we have features for recognizing the windows, body, and wheels of a car, each represented by a single neuron. In the middle, these combine to form a car feature. But along the right, we have neurons which primarily represent various dog features. The car feature is spread across these neurons, making each of them polysemantic.

So for the third layer depicted above, we have no single neuron representing cars. Instead, the network represents the feature by activating each polysemantic dog/car neuron some small amount. Superposition is when we spread a single conceptual feature across multiple neurons like this.

So in my discussion group, when someone asked, “What’s the difference between polysemanticity and superposition exactly? Are they two different words for the same thing? Or can you have one without the other?”, I thought I had a good answer. I said that in a way, they are inverse concepts. Polysemanticity is when one neuron responds to multiple features, while superposition is when one feature is spread across multiple neurons.

As for having one without the other, I gave it some thought and said, “Suppose we had a single neuron which responds to both cats and cars. Maybe when it’s positive that means cats, but when it’s negative that means cars. Both features are fully represented by this single neuron. So that neuron would be polysemantic, but there would be no superposition, since the features aren’t spread across multiple neurons.”

Differing Definitions

Some of the group did not like my answer one bit. Why not? Well, some of them were operating off a different definition of superposition. In the other paper Toy Models of Superposition, they define it as “when models represent more features than they have dimensions”, where “dimensions” simply means “neurons”.

In the example I gave, then, supposing our network somehow consisted of a single neuron which responded to both cats and cars, this would mean we have two features packed into a single dimension, making this an example of superposition.

At first, this alternate definition really confused me. The previous one made a lot more intuitive sense to me. For one thing, there’s something very concrete about being able to point at a particular feature and say “this feature is in superposition”, as we did for the car above.

But under this new definition, we simply say the network as a whole exhibits superposition, without saying anything about any particular feature, which felt a lot more abstract to me. That is, if the network represents five features but only has four neurons, then there must be superposition, but this definition isn’t telling you which feature is in superposition, or even admitting that that question makes sense.

Moreover, it also made it a lot harder for me to answer my groupmate’s question. I was suddenly much fuzzier on the distinction between polysemanticity and superposition and couldn’t quite picture one without the other.

Polysemanticity Without Superposition

Another one of my groupmates, Eyas Ayesh, swooped in to provide his own example. But since I can be a bit of an idiot, I didn’t really follow it. So I asked him to write up the example for me concretely to help me understand, which he kindly allowed me to use here. (Thanks, Eyas!)

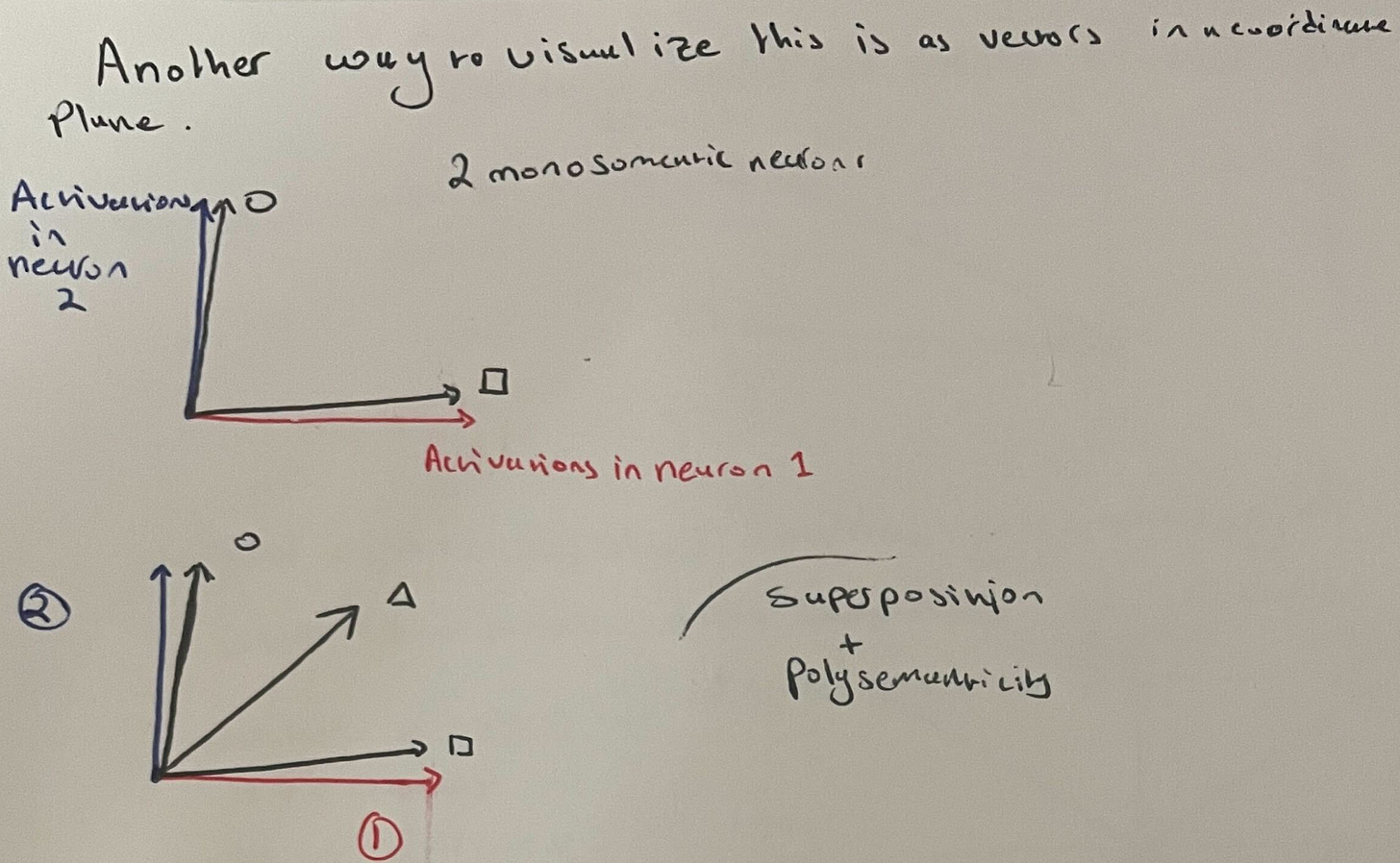
His example proceeds thuslywise¹. Suppose we have a neural network which represents two features: a square and a circle. Suppose further that each is represented by a single neuron in the network. This is a simple example of two monosemantic neurons with no superposition:

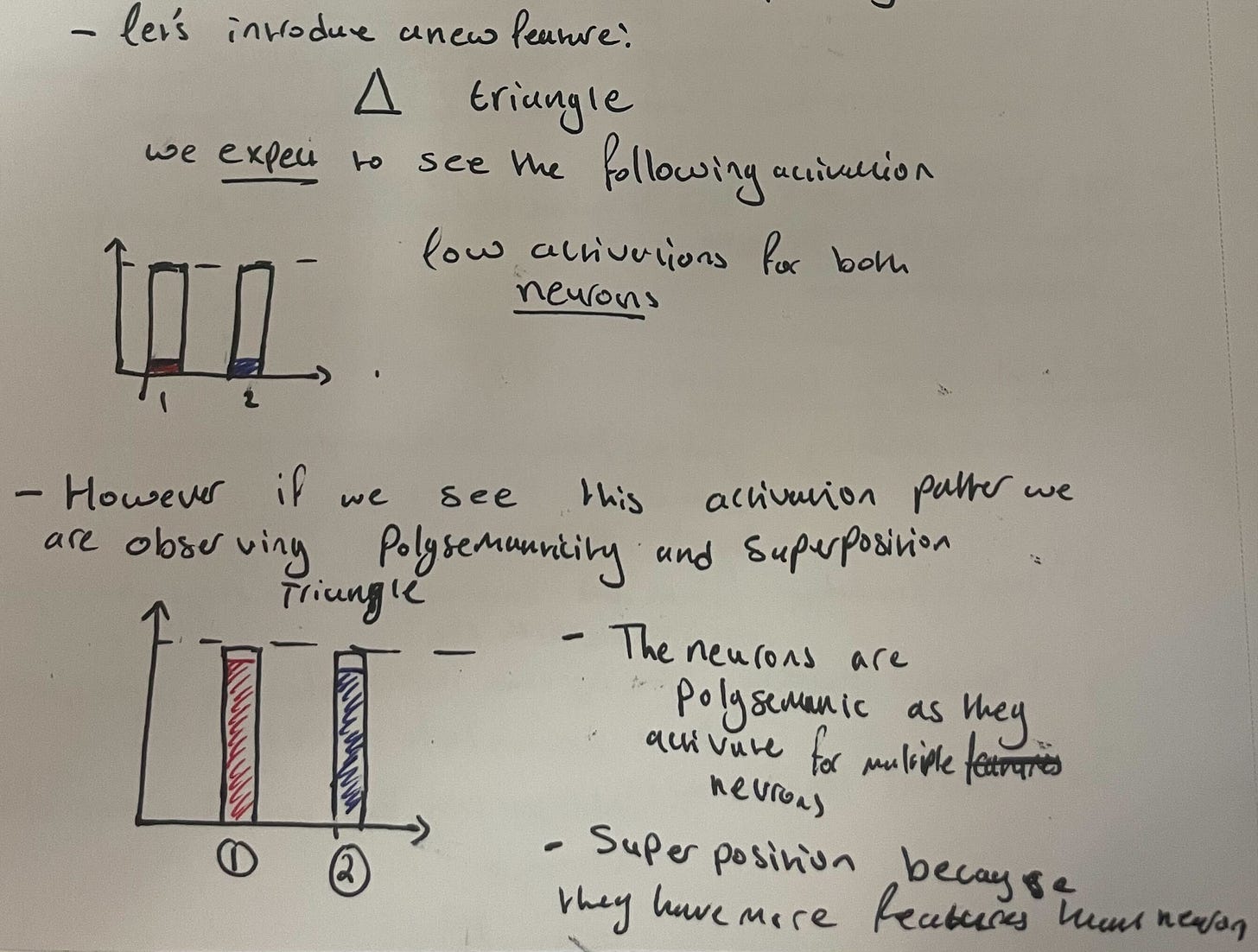
Now suppose we introduce a new feature, a triangle. Naively, we might expect neither the square neuron nor the circle neuron to activate in the presence of this input, but it’s possible that they might. The triangle feature might be represented by the dual activation of both neurons at once:

This is simple example of both polysemanticity and superposition. We have polysemanticity since both neurons respond to two different features, and we have superposition because we have three features packed into two dimensions. We can visualize this by representing neurons as basis vectors in 2D space as well:

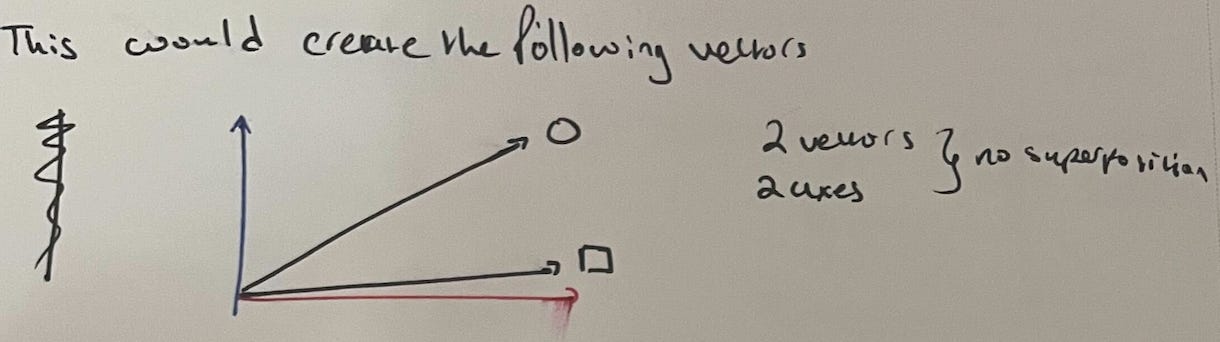
So what about polysemanticity without superposition? For this to happen, there must be only two features and two neurons; we can’t pack any extra features in. But we also need each neuron to respond to multiple features. The solution is simple: spread each feature across both neurons. In Eyas’s example, he actually has the square feature be fully contained in one neuron, while the circle is split across both, but the basic idea is the same:

Depicted with vectors:

So the first neuron is polysemantic, since it activates for both circles and squares. But since we have two features and two dimensions, there’s no superposition. More generally/abstractly, if we have n features and n neurons, each feature might be represented as a mixture of neurons, yielding polysemanticity but no superposition. Here’s an example in four dimensions:

Reconciliation

Thanks to Eyas, I now understood this alternative idea of superposition. But I was still bugged by having two different definitions. I felt like there was something more intuitive about the first definition, where superposition means a particular feature is spread across neurons. The term “superposition” for me evokes the idea of an object which is some non-trivial mixture of basis elements, which here would seemingly mean a mixture of neurons.

It sort of felt to me like the first definition was an informal one, while the latter was an attempt at formalizing it, maybe in a way that didn’t quite capture the original intention? Looking at the last image above, it sure did intuitively feel to me like those features were in superposition. Is it really intentional that this new definition excludes that case?

If we trust Neel Nanda—and we should—then the answer is yes, it is intentional! He has a glossary of standard mechanistic interpretability terms, including an entry on superposition. In it, he says:

Subtlety: Neuron superposition implies polysemanticity (since there are more features than neurons), but not the other way round. There could be an interpretable basis of features, just not the standard basis—this creates polysemanticity but not superposition.

This neatly describes the exact example Eyas gave me. Even further, it helped me understand how these two different definitions of superposition relate.

Intuitively it certainly seems like these two definitions are pointing at a similar thing, so we ought to be able to see the relationship between them. Here’s what it is. The old definition says that a feature is in superposition when it’s a non-trivial mixture of basis elements, where the neurons form our basis. The new definition says that even if we change our basis, some feature will always be forced to be a mixture of basis elements.

Look at the last image above. This system isn’t in superposition because we can choose the feature vectors to be our basis. Under this basis, no feature is a non-trivial mixture of basis elements, hence no superposition. But suppose there were five features. Then no matter what basis we picked, some feature will be a non-trivial mixture of basis elements, since we only have four dimensions!

We can rephrase the original definition of superposition from Zoom In to say “a feature is in superposition when it’s a non-trivial mixture of the privileged basis elements: the neurons”. We can generalize this definition slightly to say “the network is in superposition if under all bases, there’s always some feature which is a non-trivial mixture of basis elements”. And this latter conditions holds iff we have more features than neurons. So by a simple generalization of the first definition, we get the second. Tada!

Conclusion

All this was really just for my own understanding, rather than producing any new insight. But if you have a passing interest in mechanistic interpretability as well, maybe this post will have been of some value to you.

I’ve dug into mechanistic interpretability more generally these past few weeks aside from just trying to answer this question, and I have to say, I think I love this field! Currently it seems to me like the best approach to AI alignment we have.

Why is that? This research mostly seems to be about understanding models rather than controlling them (although this is not universally true), so how does it help in making AIs do what we want?

My answer is that most of my fear comes precisely from us not understanding what we’re doing. If we really knew how intelligence worked and were carefully engineering it ourselves to do what we want… Well, that would still be dangerous. but it would be orders of magnitude better than our current situation.

Yann LeCun says we shouldn’t worry about AI because we are engineering it. We are the ones in control. And I just don’t think this is true. Making it true would be invaluable. Current alignment methods seem to mostly consist of evaluating and fine-tuning surface-level behavior. And I just don’t think that gets you anywhere for systems which are smarter than us so long as we don’t really know what’s going on internally.

From my point of view, there are two high-level research approaches which seem to be tackling the hard part of the problem. On the theoretical side, agent foundations is an attempt at understanding how agency and intelligence really works. On the empirical side, mechanistic interpretability tries to understand the intelligent artifacts we already have.

To me, both are forms of deconfusion research. We are fundamentally confused about how intelligence works, and until we become significantly less confused, controlling AI systems will be very very hard. So my grand hope for interpretability is not so much that we find ways to intervene on a network to control its behavior (although that’s an avenue worth exploring!), but that we gain sufficient understanding of intelligence to help us build it safely.

The thing I’m about to say is wildly naive, but hey, that’s what we’re all about here. Neel Nanda has a discussion on induction heads. The exact workings of induction heads is beyond the scope of this essay, but in that video, Charles Fyre says we can imagine implementing their basic behavior using some “Markov skip-gram model”, which is to say, a somewhat more classical NLP technique.

Admittedly, Charles goes on to say that their full behavior is presumably too complex for that. But still, this really sparks my imagination. I thought, hey, has anyone tried that? Have we tried, just, literally reimplementing the behavior of small transformers to the best of our ability using more classical techniques? I feel like there could be a lot of insight there.

What would it take to understand a transformer so well that we can literally handwrite its algorithms using techniques we understand? That is my dream for interpretability. If I can dream even further, we might even get fresh insights on how intelligence works, sufficient to inspire brand new AI techniques. If timelines to AGI turn out to be longer than many of us expect, this could kick off a whole new AI paradigm, one which is more understandable and controllable.

1. https://x.com/noahtopper/status/1796002657808626004?s=46